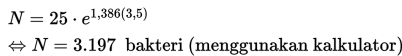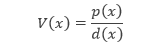Fungsi Rasional

A. Fungsi RasionalFungsi rasional adalah fungsi yang memiliki bentuk

Dengan p dan d merupakan polinomial dan d(x) ≠ 0. Domain dari V(x) adalah semua bilangan real, kecuali pembuat nol dari d.

Fungsi rasional yang paling sederhana adalah fungsi y = 1/x dan fungsi y = 1/x², yang keduanya memiliki pembilang konstanta dan penyebut polinomial dengan satu suku, serta kedua fungsi tersebut memiliki domain semua bilangan real kecuali x ≠ 0.

Fungsi y = 1/x

Fungsi ini disebut juga sebagai fungsi kebalikan karena setiap kita mengambil sembarangx (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut. Hal ini berarti x yang besar akan menghasilkan nilai fungsi yang kecil, demikian pula sebaliknya. Tabel dan grafik dari fungsi tersebut dapat dilihat seperti di bawah ini.

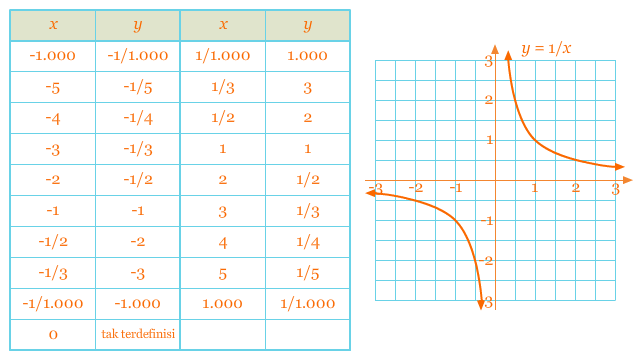
Tabel dan grafik di atas memunculkan beberapa hal yang menarik. Pertama, grafik tersebut lolos uji garis vertikal, artinya, setiap garis vertikal pada bidang koordinat Cartesius memotong grafik pada maksimal satu titik. Sehingga, y = 1/x merupakan suatu fungsi. Kedua, karena pembagian tidak terdefinisi ketika pembaginya nol, maka nol tidak memiliki pasangan, yang menghasilkan jeda pada x = 0. Hal ini sesuai dengan domain dari fungsi tersebut, yaitu semua x anggota bilangan real kecuali 0. Ketiga, fungsi tersebut merupakan fungsi ganjil, dengan salah satu cabangnya berada di kuadran I sedangkan yang lainnya berada di kuadran III. Dan yang terakhir, pada kuadran I, ketika x menuju tak hingga, nilai y menuju dan mendekati nilai nol. Secara simbolis dapat ditulis sebagaix → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-xketika x mendekati tak hingga.

Selain itu kita juga dapat mengamati bahwa ketika x mendekati nol dari kanan maka nilaiy akan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞. Sebagai catatan, tanda + atau – yang terletak di atas mengindikasikan arah dari pendekatan, yaitu dari sisi positif (+) atau dari sisi negatif (–).

---

Contoh 1: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Untuk y = 1/x dalam kuadran III,

1. Deskripsikan sifat dari ujung grafik fungsi tersebut.
2. Deskripsikan apa yang terjadi ketika x mendekati nol.

Pembahasan Serupa dengan sifat grafiknya pada kuadran I, kita mendapatkan

1. Ketika x mendekati negatif tak hingga, nilai y akan mendekati nol. Apabila disimbolkan x → –∞, y → 0.
2. Ketika x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga dapat dituliskan dengan x → 0–, y → –∞.

---

Fungsi y = 1/x²

Dari pembahasan sebelumnya, kita dapat menduga bahwa grafik dari fungsi ini akan jeda ketika x = 0. Akan tetapi karena kuadrat dari sembarang bilangan negatif adalah bilangan positif, cabang-cabang dari grafik fungsi ini akan berada di atas sumbu-x. Perhatikan bahwa fungsi y = 1/x² merupakan fungsi genap.

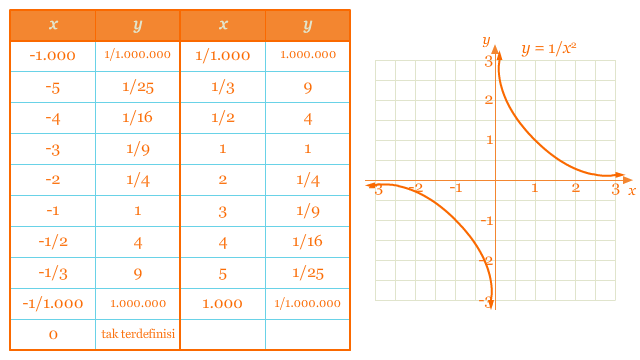
Serupa dengan y = 1/x, nilai x yang mendekati positif tak hingga, menghasilkan y yang mendekati nol: x → ∞, y → 0. Hal ini merupakan salah satu indikasi dari sifat asimtot dalam arah horizontal, dan kita mengatakan y = 0 merupakan asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,

Asimtot HorizontalDiberikan suatu konstanta k, garis y = k merupakan asimtot horizontal dari fungsi V(x) jika x bertambah tanpa batas, menyebabkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.

Pada gambar (a) di bawah ini menunjukkan garis asimtot horizontal pada y = 1, yang menggambarkan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan. Gambar (b) menunjukkan garis asimtot horizontal pada y = –2, yang menggambarkan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.

---

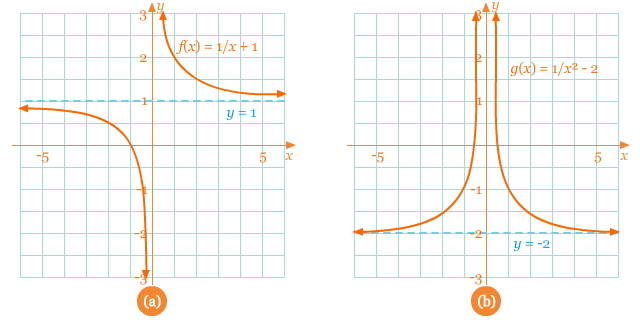
Contoh 2: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional

Berdasarkan gambar (b) di atas, gunakan notasi matematika untuk,

1. Mendeskripsikan sifat dari ujung grafik tersebut.
2. Mendeskripsikan apa yang terjadi ketika x mendekati nol.

Pembahasan

1. Ketika x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
2. Ketika x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.

---

Dari contoh 2b di atas, kita dapat melihat bahwa ketika x mendekati nol, g menjadi sangat besar dan semakin bertambah tak terbatas. Hal ini merupakan indikasi dari sifat asimtot dalam arah vertikal, dan selanjutnya kita menyebut garis x = 0 merupakan asimtot vertikal untuk g (x = 0 juga merupakan asimtot vertikal untuk f). Secara umum,

Asimtot VertikalDiberikan suatu konstanta h, garis x = h merupakan asimtot vertikal untuk fungsi V jika x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: ketika x → h+, V(x) → ±∞ atau ketika x → h–, V(x) → ±∞.

Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah berguna karena grafik y = 1/x dan y = 1/x² dapat ditransformasi dengan menggesernya ke arah vertikal ataupun gorizontal. Fungsi,

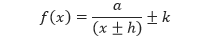
merupakan bentuk pergeseran dari fungsi y = 1/x. Sedangkan fungsi,

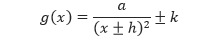
merupakan bentuk pergeseran dari fungsi y = 1/x². Selanjutnya perhatikan contoh berikut.

---

Contoh 3: Menuliskan Persamaan dari Fungsi Rasional

Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, kemudian gunakan grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggap |a| = 1.

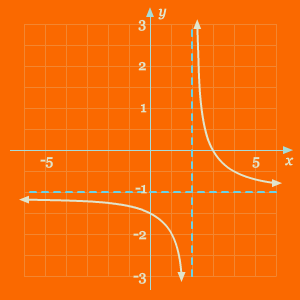
Pembahasan Dari grafik di atas, kita dapat melihat bahwa grafik tersebut merupakan pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan dan ke bawah sejauh 1 satuan. Sehingga asimtot horizontal dan vertikal dari grafik tersebut secara berturut-turut adalahy = –1 dan x = 2. Sehingga, persamaan dari grafik di atas adalah

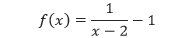
yang merupakan bentuk pergeseran dari fungsi y = 1/x

1. fungsi polinomial

 atau suku banyak (juga ditulis sukubanyak) adalah pernyataan matematika yang melibatkan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien. Sebuah polinomial dalam satu variabel dengan koefisien konstan memiliki bentuk seperti berikut:

${\displaystyle a_{n}x^{n}+\ldots +a_{2}x^{2}+a_{1}x+a_{0}}$

Pangkat tertinggi pada suatu polinomial menunjukkan orde atau derajat dari polinomial tersebut.

Grafik polinomial

Sebuah fungsi polinomial dalam satu variabel real dapat dinyatakan dalam grafik fungsi.

• Grafik dari polinomial nol

f(x) = 0

adalah sumbu x.

• Grafik dari polinomial berderajat nol

f(x) = a₀, dimana a₀ ≠ 0,

adalah garis horizontal dengan y memotong a₀

• Grafik dari polinomial berderajat satu (atau fungsi linear)

f(x) = a₀ + a₁x , dengan a₁ ≠ 0,

adalah berupa garis miring dengan y memotong di a₀ dengan kemiringan sebesar a₁.

• Grafik dari polinomial berderajat dua

f(x) = a₀ + a₁x + a₂x², dengan a₂ ≠ 0

adalah berupa parabola.

• Grafik dari polinomial berderajat tiga

f(x) = a₀ + a₁x + a₂x², + a₃x³, dengan a₃ ≠ 0

adalah berupa kurva pangkat 3.

• Grafik dari polinomial berderajat dua atau lebih

f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ , dengan a_n ≠ 0 and n ≥ 2

adalah berupa kurva non-linear.

Ilustrasi dari grafik-grafik tersebut adalah di bawah ini.

• 

  Polinomial berderajat 2:
  f(x) = x² - x - 2 = (x+1)(x-2)
 
• 

  Polinomial berderajat 3:
  f(x) = x³/4 + 3x²/4 - 3x/2 - 2 = 1/4 (x+4)(x+1)(x-2)
 
• 

  Polinomial berderajat 4:
  f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5
 
• 

  Polinomial berderajat 5:
  f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2
 
• 

  Polinomial berderajat 6:
  f(x) = 1/30 (x+3.5)(x+2)(x+1)(x-1)(x-3)(x-4) + 2
 
• 

  Polinomial berderajat 7:
  f(x) = (x-3)(x-2)(x-1)(x)(x+1)(x+2)(x+3)

Polinomial dan kalkulus[sunting | sunting sumber]

Artikel utama untuk bagian ini adalah: Kalkulus dengan polinomial

Untuk menghitung turunan dan integral dari polinomial tidaklah terlalu sulit. Untuk fungsi polinomial

${\displaystyle \sum _{i=0}^{n}a_{i}x^{i}}$

maka turunan terhadap x adalah

${\displaystyle \sum _{i=1}^{n}a_{i}ix^{i-1}}$

dan integral tak tentu terhadap x adalah

${\displaystyle \sum _{i=0}^{n}{a_{i} \over i+1}x^{i+1}+c.}$

Contoh 1:

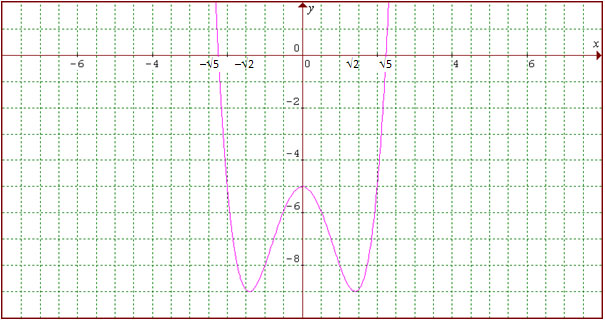
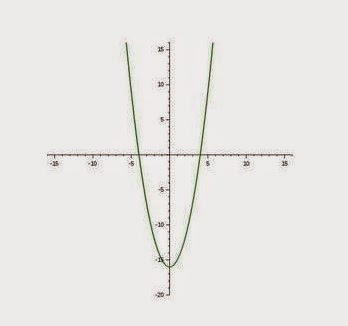
Gambarlah grafik fungsi y = x4 – 4x2 – 5!

Titik potong dengan sumbu-x (y = 0):

x4 – 4x2 – 5 = 0

(x2 – 5)(x2 + 1) = 0

x2 – 5 = 0 atau x2 + 1 = 0

x2 = 5 atau x2 = –1

karena x2 = –1 tidak memenuhi untuk x bilangan Real, maka yang digunakan x2 = 5 → x = ±√5

Jadi, titik potong dengan sumbu-x: (√5, 0) dan (–√5, 0)

Titik potong dengan sumbu-y (x = 0):

y = 04 – 4(0)2 – 5 = –5

Jadi, titik potong dengan sumbu-y: (0, –5)

Titik ekstrim (y’ = 0)

y’ = 0

4x3 – 8x = 0

4x(x2 – 2) = 0

4x = 0 atau x2 – 2 = 0

x = 0 atau x = ±√2

Untuk x = 0 → y = 04 – 4(0)2 – 5 = –5

Untuk x = –√2 → y = (–√2)4 – 4(–√2)2 – 5 = 4 – 4(2) – 5 = –9

Untuk x = √2 → y = (√2)4 – 4(√2)2 – 5 = 4 – 4(2) – 5 = –9

Jadi, titik-titik ekstrimnya: (0,  –5), (–√2, –9), (√2, –9)

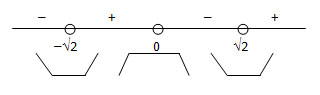
Sketsa:

Jika x = 1 → y’ = 4(1)3 – 8(1) = –4 (negatif)

Tanda positif dan negatif berselang-seling. Karena x = 1 hasilnya negatif, maka antara 0 dan √2 diberi tanda negatif, antara –√2 dan 0 diberi tanda positif, di sebelah kiri –√2 diberi tanda negatif, dan di sebelah kanan √2 diberi tanda positif.

Jika bertanda negatif, gambar garis turun, jika bertanda positif, gambar garis naik.

Gambar Fungsi:

Contoh 2:

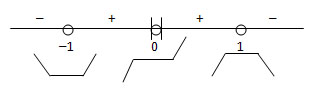
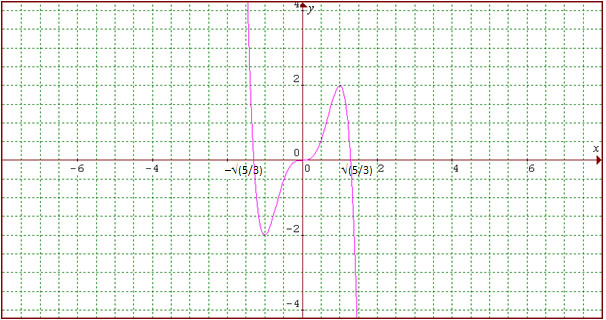
Gambarlah grafik fungsi y = 5x3 – 3x5!

Titik potong dengan sumbu-x (y = 0):

5x3 – 3x5 = 0

x3(5 – 3x2) = 0

x3 = 0 atau 5 – 3x2 = 0

x = 0 atau 3x2 = 5

x = 0 atau x = ±√(5/3)

Jadi, titik potong dengan sumbu-x: (0, 0), (–√(5/3), 0), (√(5/3), 0)

Titik potong dengan sumbu-y (x = 0):

y = 5(0)3 – 3(0)5 = 0

Jadi, titik potong dengan sumbu-y: (0, 0)

Titik ekstrim (y’ = 0):

y’ = 0

15x2 – 15x4 = 0

15x2(1 – x2) = 0

15x2 = 0 atau 1 – x2 = 0

Untuk 15x2 = 0 → x = ±0 (batas rangkap untuk x = 0)

Untuk 1 – x2 = 0

x2 = 1 → x = ±√1 = ± 1

x = 0 → y = 0

x = –1 → y = 5(–1)3 – 3(–1)5 = –5 + 3 = –2

x = 1 → y = 5(1)3 – 3(1)5 = 5 – 3 = 2

Jadi, titik-titik ekstrimnya: (0, 0), (–1, –2), (1, 2)

Sketsa:

Jika x = 10 → y’ = 15(10)2 – 15(10)4 = 1500 – 1500000 → hasilnya negatif

Karena 0 merupakan batas rangkap, maka tidak merubah tanda. Karena untuk x = 0 hasilnya negatif, di sebelah kanan 1 diberi tanda negatif, antara 0 dan 1 diberi tanda positif, antara –1 dan 0 tandanya tetap positif, dan di sebelah kiri –1 diberi tanda negatif.

Gambar Fungsi:

Contoh 3:

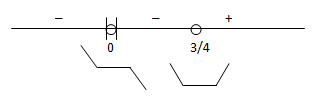
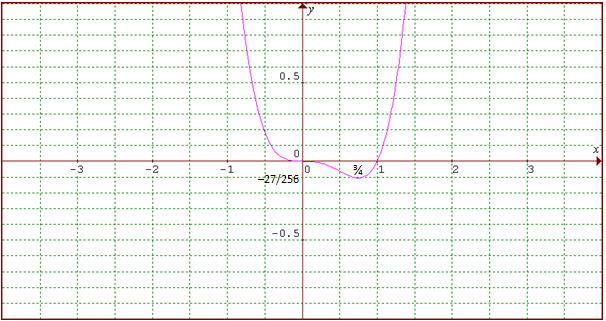
Gambarlah grafik fungsi y = x4 – x3!

Titik potong dengan sumbu-x (y = 0):

x4 –x3 = 0

x3(x – 1) = 0

x = 0 atau x – 1 = 0

x = 0 atau x = 1

Jadi, titik potong dengan sumbu-x: (0, 0), (1, 0)

Titik potong dengan sumbu-y (x = 0):

y = 04 – 03 = 0

Jadi, titik potong dengan sumbu-y: (0, 0)

Titik ekstrim (y’ = 0):

y’ = 0

4x3 – 3x2 = 0

x2(4x – 3) = 0

x2 = 0 atau 4x – 3 = 0

x = ±0 (batas rangkap) atau 4x = 3 → x = ¾

x = 0 → y = 0

x = ¾ → y = (¾)4 – (¾)3 = 81/256 – 27/64 = 81/256 – 108/256 = –27/256

Jadi, titik ekstrimnya: (0, 0), (3/4, –27/256)

Sketsa:

Jika x = 1 → y’ = 4(1)3 – 3(1)2 = 4 – 3 = 1 (positif)

Jadi, daerah di sebelah kanan ¾ bertanda positif, antara 0 hingga ¾ bertanda negatif, dan di sebelah kiri 0 tandanya tetap negatif karena 0 merupakan batas rangkap.

Gambar Fungsi:

2. FUNGSI LINEAR

Fungsi linier adalah fungsi polinom yang variable bebasnya memiliki pangkat paling tinggi adalah satu.: Y = a0+a1x1, Y variable terikat, x variable bebas.

a0 : konstanta,nilai positif, negatif, atau nol
a1 : konstanta, nilai positif, negatif, atau nol.

Untuk nilai a0 dan a1 yang memungkinkan positif, negatif atau nol, maka alternatif yang
mungkin untuk fungsi linier : Y =a1 + a1x1, yaitu: a0 = + ; a1 = +

Misal : a0= 4 dan a1= 2
Y = a0 + a1x maka Y= 4 + 2x

• PENGGAMBARAN FUNGSI LINEAR

Penggambaran fungsi linier dari berbagai alternatif untuk a0 dan a1 = 2
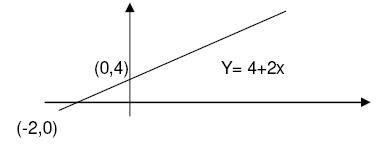
a. Y = 4 + 2 x ;dua buah titik yang dibutuhkan untuk menggambarkannya
(0,4) dan (-2,0)

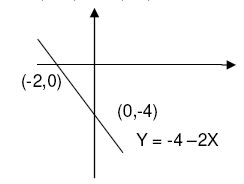
b. Y = 4 –2x; dua buah titik yang dibutuhkan untuk menggambarkannya
(0,4) dan (2,0)

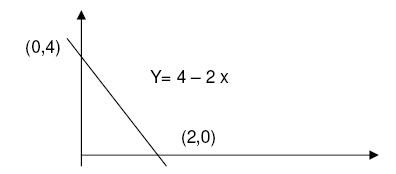
c. Y = -4 + 2 x dua buah titik yang dibutuhkan untuk menggambarkannya

(0,-4) dan (2,0)

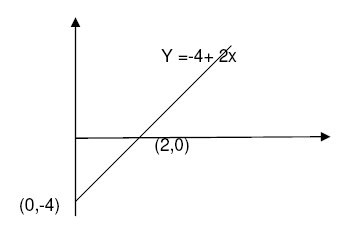
d. Y = -4 – 2X dua buah titik yang dibutuhkan untuk menggambarkannya
(0,-4) dan (2,0)

Kesimpulan: Untuk fungsi linier Y = a0 + a1X a0 : intersep dan a1 :
gradien/kemiringan.

Intersep a0 merupakan titik potong antara fungsi linier dengan sumbu Y di atas
sumbu datar X

• ao positif maka perpotongan fungsi linier dengan sumbu Y di
atas sumbu datar X

• a0 negatif maka perpotongan fungsi linier dengan sumbu Y di
bawah sumbu datar X

• Jika a0 nol maka perpotongan antara fungsi linier dengan sumbu
Y pada titik (0,0)
Gradien a1 merupakan kemiringan fungsi linier terhadap sumbu X

• HUBUNGAN 2 FUNGSI LINIER

Ada dua fungsi linier dimana fungsi linier pertama yaitu, Y = a0 + a1 X dan
fungsi linier yang kedua yaitu Y’ = a0’+ a1’ X. Kedua fungsi linier berada dalam berbagai keadaan.

1. Berhempit

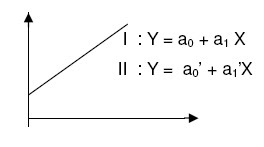
Karena berimpit, maka a0 = a0’ dan a1 = a1’
Contoh: fungsi linier I : Y = 4 + 2X
Fungsi linier II : 2Y = 8 + 4 X, intersep 8/2 = 4 ; gradien 4/2 = 2

2. Sejajar

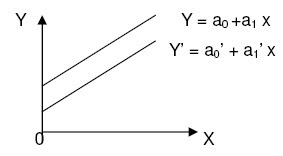
karena sejajar, maka a0= a1’ dan a1 = a1’

Contoh: fungsi linear I : Y = 4 + 4 X, intersep 4 dan gradien 4
Fungsi linier II : Y = 2 + 4 X, intersep 2 dan gradien 4

3. Berpotongan

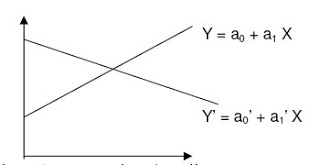
Karena berpotongan, maka a1 = a1’

Contoh : fungsi linear I Y = 4 + 4X, intersep 4, gradien 4 Fungsi linear II Y = 2 – 4 X, intersep 2 , gradien –4

4. Titik Potong Fungsi Linier

Untuk fungsi linear yang saling berpotongan dapat dilakukan dengan cara:
• Subsitusi
• Eliminasi
• Determinan

Contoh:
Carilah titik potong dari dua garis yang berpotongan yaitu 2X + 3 Y = 4 dan X + 2 Y = 1

Jawab:

1. Cara subsitusi
2X + 3Y = 4 ………….(1)
x + 2 Y= 1 >>>  x = 1 – 2 Y …………..(2)

Masukkan (2) pada (1)

2 X + 3 Y = 4                             Sehingga X = 1 – 2 Y
2 ( 1-2 Y) + 3Y = 4                                   X = 5
2-4Y+3Y = 4
2 – Y = 4
Y = -2

2. Eliminasi

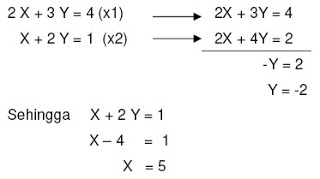
3. Determinan
2X + 3Y = 4
X + 2Y = 1
Baik dengan cara eliminasi, substitusi maupun determinan, hasilnya X dan Y sama.

• PENAMAAN FUNGSI LINIER

1. Jika diketahui dua buah titik yaitu A (x1,y1) dan B (x2,y2)
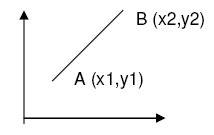
Gambar: 

 Untuk mengetahui garis yang tepat melalui kedua titik tersebut dengan rumus :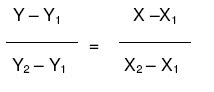 

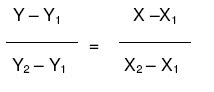
2. Jika diketahui sebuah titik A (X1,Y1) dan gradien/kemiringannya m
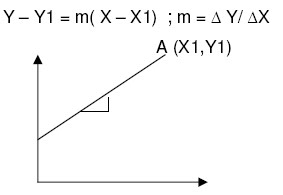
Rumus: 

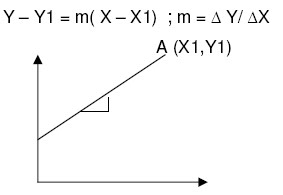
3. FUNGSI KUADRAT

Kurva fungsi kuadrat y = f( x ) = ax2 + bx + c, a tidak sama dengan nol ( 0 ) berbentuk parabola.

Jika nilai a > 0 maka parabola terbuka ke atas dan mempunyai nilai ekstrem minimum

Jika nilai a < 0 maka parabola terbuka ke bawah dan mempunyai nilai ekstrem maksimum

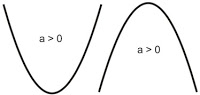
Koordinat titik puncak / titik ekstrem / titik stationer / titik balik parabola adalah ( Xp , Yp )dengan :

Xp = absis ( x ) titik puncak = sumbu simetri = absis ( x ) saat mencapai nilai maksimum/minimum
Yp = ordinat ( y ) titik puncak = nilai ekstrem/nilai stationer/nilai maksimum/nilai minimum

Sketsa Grafik Fungsi Kuadrat

Langkah-langkah dalam membuat sketsa grafik fungsi kuadrat/parabola ( y  = ax2+ bx + c ) :

1. menentukan titik potong grafik dengan sumbu x → y = 0

kemudian difaktorkan sehingga diperoleh akar-akarnya yaitu x1 dan x2 . jika kesusahan dalam memfaktorkan coba di cek dulu nilai D nya….

jika D < 0 maka fungsi tersebut memang tidak mempunyai akar-akar persamaan fungsi kuadrat sehingga sketsa grafik fungsi kuadrat tidak memotong sumbu x

jika D > 0 maka fungsi tersebut mempunyai akar-akar persamaan fungsi kuadrat namun kita kesulitan dalam menentukannya… bisa jadi karena angkanya yang susah difaktorkan atau faktornya dalam bentuk desimal. Akar-akarnya dapat kita cari dengan rumus abc :

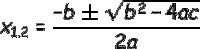
etelah kita mendapatkan nilai x1 dan x2 maka titik potong grafik fungsi kuadrat dengan sumbu x :
( x1 , 0 ) dan ( x2 , 0 )

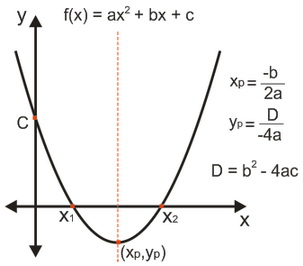
2. menentukan titik potong grafik dengan sumbu y → x = 0karena x = 0 maka y = c dan titik potong dengan sumbu y = ( 0 , c )

3. menentukan sumbu simetri ( xp ) dan titik ekstrem ( yp )

dari penentuan sumbu simetri ( xp ) dan nilai eksterm   ( yp ) diperoleh titik puncak grafik fungsi kuadrat/parabola : ( Xp , Yp )

Posisi grafik fungsi kuadra sumbu x
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :

D > 0 → grafik fungsi kuadrat memotong sumbu x di dua titik
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x

dengan menggabungkan dengan nilai a nya dapat dibuat sketsa grafik fungsi kuadrat: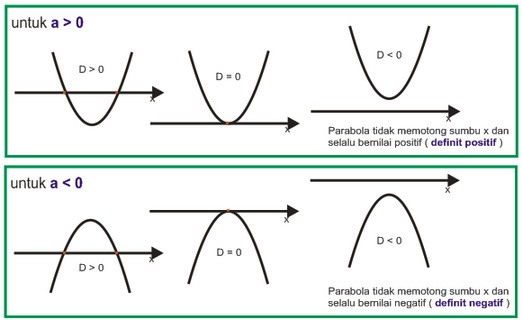

C. Persamaan Fungsi Kuadrat / Parabola

1. Diketahui tiga titik sembarang

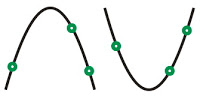
Rumus : y =  ax2 + bx + c 

nilai a, b dan c ditentukan dengan eliminasi.

2. Parabola memotong sumbu x di dua titik ( x1 , 0 )dan ( x2 , 0 ) dan melalui satu titik sembarang.

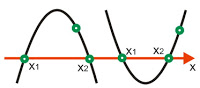
 Rumus : y = a ( x – x1 ).( x – x2 )

nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.

3. Parabola menyinggung sumbu x di satu titik ( x1 , 0 ) dan melalui satu titik sembarang.

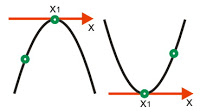
Rumus : y = a ( x – x1 )2 
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.

4. Parabola melalui titik puncak ( xp , yp ) dan melalui satu titik sembarang.

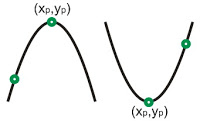
Rumus : y = a ( x – xp )2 + yp
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.

D. Hubungan Kurva Persamaan Kuadrat / Parabola dan Persamaan Garis Lurus

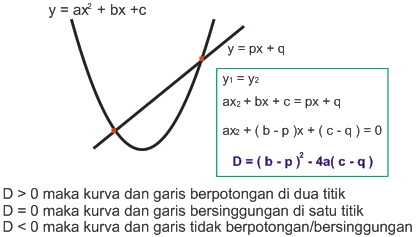
GRAFIK FUNGSI LINIER DAN KUADRAT

Grafik Fungsi Linier dan Kuadrat – Pada pelajaran sebelumnya, telah dibahas bagaimana menyelesaikan dan menggambar grafik fungsi linier & grafik fungsi kuadrat. Oleh karena itu, pada pelajaran ini, kalian akan belajar tentang bagaimana menentukan titik potong serta nilai maksimum dan minimum dari suatu fungsi dengan menggunakan grafik.

Ingatlah kembali metode menggambar grafik fungsi linear dan grafik fungsi kuadrat.

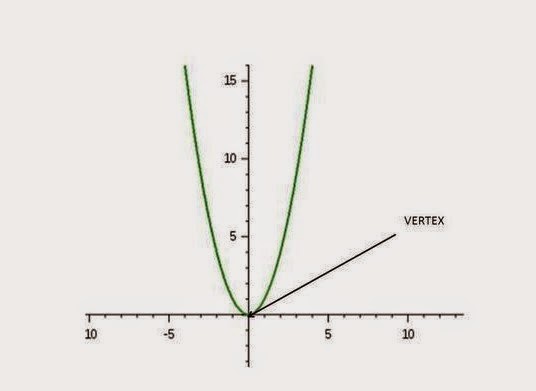
Grafik persamaan kuadrat y = ax2 + bx + c selalu berbentuk parabola. Sebagai contoh adalah grafik y = x2.

Titik puncak dari suatu grafik fungsi kuadrat adalah titik yang terletak pada sumbu simetri, dimana titik tersebut dilalui oleh parabola. Selanjutnya, jika koefisien dari x2 bernilai positif, maka titik puncaknya merupakan titik terendah dalam grafik. Akan tetapi, jika koefisien dari x2bernilai negatif, maka titik puncaknya merupakan titik tertinggi dalam grafik.

Nilai maksimum dari suatu fungsi kuadrat didefinisikan sebagai nilai terbesar yang dapat dicapai oleh fungsi kuadrat tersebut. Sedangkan nilai minimumnya didefinisikan sebagai nilai terkecil yang dapat dicapai oleh fungsi kuadrat tersebut.

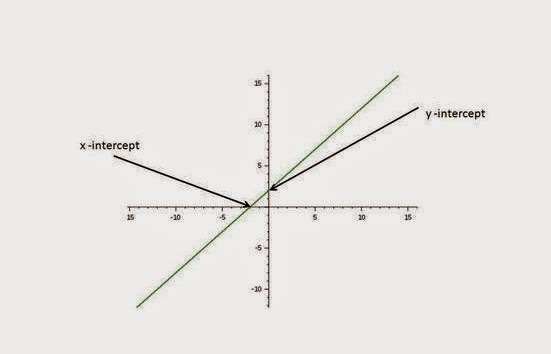
Grafik persamaan linear y = ax + b selalu berupa garis lurus. Sebagai contoh adalah grafik y = x + 2.

Absis dari titik potong dengan sumbu X diperoleh ketika y = 0. Sedangkan ordinat dari titik potong dengan sumbu Y diperoleh ketika x = 0.

Lebih lanjut, dalam pelajaran ini kalian akan belajar untuk menganalisa suatu grafik fungsi dan secara khusus akan belajar tentang bagaimana untuk :

       •menentukan nilai maksimum dan minimum serta titik potong dari suatu fungsi kuadrat dengan menggunakan grafik

       •menentukan titik potong dari sutu persamaan dengan menggunakan grafik

Contoh 1 :

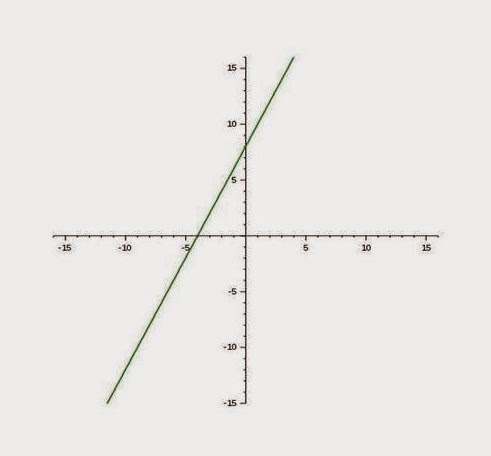
Gambarlah grafik y = 2x + 8 !

Selanjutnya, tentukan titik potong dengan sumbu X!

Penyelesaian :

Perhatikan grafik y = 2x + 8 pada gambar di bawah!

Seperti yang terlihat pada grafik, nilai y = 0 saat x = -4.

Dengan demikian, titik potong grafik dengan sumbu X adalah (-4,0). Hal ini dapat diperiksa kebenarannya dengan cara mensubtitusikan y = 0 ke dalam persamaan.

                0 = 2x + 8

                x  = -4

Contoh 2 :

Gambarlah grafik y = (x-4)(x+4) dan tentukan titik potong antara grafik dengan sumbu Y!

Penyelesaian :

Perhatikan grafik y = (x-4)(x+4) pada gambar di bawah!

Seperti yang terlihat pada grafik, nilai x = 0 saat y = -16.

Dengan demikian, titik potong grafik dengan sumbu Y adalah (0,-16). Hal ini dapat diperiksa kebenarannya dengan cara mensubtitusikan x = 0 ke dalam persamaan.

                y = (0-4)(0+4)

                y = -16

Lebih lanjut, grafik tersebut akan mempunyai nilai minimum pada titik (0,-16). Hal ini terjadi karena titik tersebut merupakan titik terendah yang dapat dicapai oleh grafik.

Dengan demikian, dapat disimpulkan bahwa sebuah persamaan kuadrat hanya dapat mempunyai nilai maksimum atau minimum saja, tetapi tidak keduanya.

4. FUNGSI KUBIK

Fungsi kubik atau fungsi berderajat tiga ialah fungsi yang pangkat tertinggi dari variabelnya adalah pangkat tiga. Setiap fungsi kubik setidak - tidaknya mempunyai sebuah titik belok (inflextion point), yaitu titik peralihan bentuk kurva dari cekung menjadi cembung atau cembung menjadi cekung. Selain titik belok, sebuah fungsi kubik mungkin pula mempunyai satu titik ekstrim (maksimum atau minimum) atau titik dua ekstrim (maksimum atau minimum). Ada tidaknya titik ekstrim dalam suatu fungsi kubik tergantung pada besarnya nilai-nilai b, c, dan d di dalam persamaannya. Dengan demikian terdapat beberapa kemungkinan mengenai bentuk kurva suatu fungsi kubik. Fungsi-fungsi kubik hanya mempunyai titik belok, tanpa titik ekstrim.

 fungsi kubik  memiliki bentuk:

dengan a bernilai tidak nol; atau dengan kata lain merupakan suatu polinomial orde tiga. Turunan dari suatu fungsi kubik adalah suatufungsi kuadrat. Integral dari suatu fungsi kubik adalah fungsi pangkat empat (kuartik).

Menetapkan ƒ(x) = 0 menghasilkan persamaan kubik dengan bentuk:

Biasanya, koefisien a, b, c, dan d merupakan bilangan riil. Untuk menyelesaikan persamaan kubik, caranya dengan mencari akar (nilai nol) dari fungsi kubik.

Fungsi Kubik

Mencari :         

1. Titik Ekstrims
2. Titik Belok

Y = f(X)

v  Titik Ekstrims pada saat Y^’ = 0

v  Titk Maksimum : Y^’’ < 0, pada Y^’ =0

v  Titk Minimum : Y^’’ > 0, pada Y^’ = 0

v  Titik belok : Y^’’ = 0 , kemudian substitusikan ke fungsi asal, yi  Y = f(X)

Misal : C =1/3Q³ -3Q² +8Q +5
C = Y dan Q = X (analogi rumus)

Penyelesaian :

C^’ = 0 , maka 0 = Q² -6Q +8

0 = (Q – 4) (Q – 2)

Q₁ = 4 dan Q₂ = 2

C^’’ = 0 , maka 0 = 2Q – 6

Q₁ = 4, maka 0 = 2 (4) – 6 = 2 ;(2>0)

Pada Q₁ = 4 merupakan titik minimum

Q₁ = 4 ;C=1/3(4)³ – 3(4)² +8(4) +5 =10,33

Jadi pada Q₁ =4,merupakan titik minimum pada (4 ; 10,33)

Q₂ = 2 , pada C^’’ = 2(2)-6 = -2 ;(-2<0)

Sehingga pada Q₂ = 2 merupakan titik maksimum .

Q₂ = 2, maka C = 1/3(2)³ – 3(2)² +B(2)+5 = 11,67

Titik maksimum pada (2 ; 11,67)

Mencari titik belok

Titik belok pada saat C^’’ = 0

C^’’ = 2Q -6 ; 2Q -6 = 0, maka Q =3

Q = 3 , maka C =1/3(3)³ – 3(3)² =*(3) +5 = 11

Titik belok pada (3 ; 11)

APLIKASI DIFERENSIAL

1. Elastisitas Permintaan
2. Elastisitas Penawaran
3. Elastisitas Produksi
4. Biaya Marjinal
5. Penerimaan Marjinal
6. Analisis Keuntungan Maksimum

Elastisitas Permintaan

E_d = EQ_d = lim  (∆Q_d /Q_d ) =  dQ_d . P

       EP    ∆p  0  (∆P/ P )           dP    Q_d

Sifat elastisitas :

[E_d] > 1 = elastis ; ∆Q_d > ∆P

[E_d] < 1 = inelastis ; ∆Q_d < ∆P

[E_d] = 1 = unitary elastis ; ∆Q_d = ∆P

Contoh Soal :

Permintaan suatu barang : Q_d = 25 – 3P²

Apabila P = 5, berapa elastisitas permintaannya :

Q_d = 25 – 3P²  ; Q^’_d = -6P

E_d = -6 P. P

            25 – 3P²  = 3 (elastik)

Contoh : elastisitas penawaran dan elastisitas produksi (baca di buku Matematika Terapan untuk Bisnis dan Ekonomi ; Dumairy ; BPFE Yogyakarta).

Elastisitas Penawaran

Suatu koefisien yang menjelaskan besarnya perubahan jumlah barang yang ditawarkan berkenaan adanya perubahan harga.

E_s = EQ_s = lim  (∆Q_s /Q_s ) =  dQ_s . P

       EP   ∆p  0  (∆P/ P )            dP    Q_s

Elastisitas Produksi

Suatu koefisien yang menjelaskan besarnya perubahan jumlah output yang dihasilkan akibat adanya perubahan jumlah input.

E_p = EP = lim  (∆P /P ) =  dP . X

       EX    ∆x  0  (∆X/ X )    dX   P

P = output

X = input

BIAYA MARJINAL

Merupakan biaya tambahan yang dikeluarkan utk menghasilkan satu unit tambahan produk.

MC = C^’ = dC

                dQ

PENERIMAAN MARJINAL

Adalah penerimaan tambahan yang diperoleh berkenaan bertambahnya satu unit output yang diproduksi atau terjual.

MR = R^’ = dR

                  dQ

Biaya Marjinal

• C = Q³ – 3Q² + 4Q +4
• MC = C^’ = 3Q² – 6Q +4
• MC minimum jika MC^’ = 0
• MC^’ = 6Q -6 =0, maka Q = 1 dan nilai C = 1³ – 3(1)^{2 +}4(1) + 4 = 6

Analisis Keuntungan Maksimum

∏ = R – C = f(Q)

 ∏ optimum apabila ∏^’ = 0 atau MR =MC

Jika ∏^’’ < 0 pada ∏ maksimum , maka keuntungan maksimum

Jika ∏^’’ > 0 pada ∏ minimum , maka kerugian maksimum

Contoh soal:

R =-2Q² + 1000Q
C =- Q³ – 59Q² + 1315Q + 2000

• Carilah Q yang memberikan keuntungan maksimum dan berapa keuntungan maksimum tersebut.

Jawab:

∏^’ = 0 ; -3Q² + 114Q – 315 =0

-Q² +38Q – 105 = 0

(-Q +3) (Q-35) =0

Q₁ = 3 dan Q₂ = 35

∏^’’ = -6Q + 114

Jika Q₁ = 3 , ∏^’’ =-6(3) + 114 = 96>0

Jika Q₂ =35, ∏^’’  = -6(35) + 114

 = -96<0

Karena ∏^’’ <0 utk Q = 35 akan menghasilkan keuntungan maksimum sebesar :

∏ =-(35)³ +57(35)² -315(35) – 2000 = 13.92

5. Fungsi Eksponen (pangkat)

Fungsi eksponen adalah fungsi yang mempunyai bentuk umum y = f (x) = kax dengan x ϵ Ɍ, kdana suatu konstanta dan a > 0 serta a ≠ 0.

Agar kamu lebih paham cara membedakan fungsi yang termasuk fungsi eksponen, perhatikan beberapa fungsi berikut.
f (x) = 8 x (fungsi eksponen)
f (x) = x 8 (bukan fungsi eksponen)
f (x) = (12)x (fungsi eksponen)

Sifat-Sifat Fungsi Eksponen

• Diketahui fungsi eksponen y = f (x) = kax, maka domainnya (daerah asalnya) adalah himpunan seluruh bilangan nyata, Df = {x | x ϵ Ɍ}.

• Daerah hasilnya (rangenya) adalah himpunan seluruh bilangan nyata (real) positif, Rf = {y | y > 0,y ϵ Ɍ}.

• Grafik fungsinya selalu memotong sumbu y di titik (0, 1).

• Fungsi f (x) = ax merupakan fungsi naik untuk a > 1 dan merupakan fungsi turun untuk 0 < a < 1, serta merupakan fungsi konstan untuk a = 1.

• Grafik fungsi tidak bisa memotong sumbu x . Sumbu x merupakan asimtot datar.

Bentuk-Bentuk Fungsi Eksponen

Fungsi eksponen dibagi menjadi dua, yaitu:

• Berbentuk f (x) = a x dengan a > 1, a ϵ Ɍ dan x ϵ Ɍ.

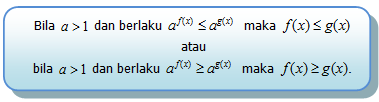
Fungsi Eksponen f (x) = a x untuk a > 1 disebut sebagai fungsi monoton naik, sebab jika x1 <x2maka ax1 < ax2.

Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut:

• Berbentuk f (x) = a x dengan 0 < a < 1, a ϵ Ɍ dan x ϵ Ɍ.

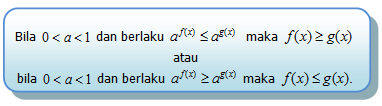
Fungsi Eksponen f (x) = a x untuk 0 < a < 1 disebut sebagai fungsi monoton turun, sebab jikax1> x2 maka ax1 > ax2.

Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut:

Penerapan Fungsi Eksponen

• Fungsi Pertumbuhan Eksponensial

y = b. a x dengan a = 1 + r

Keterangan:
b = jumlah awal (ketika x = 0)
a = faktor pertumbuhan (a > 1)
r = laju pertumbuhan per selang waktu T.
y = jumlah setelah selang waktu t
x = fraksi dengan x = tT

• Fungsi Penyusutan Eksponensial

y = b. a x dengan a = 1 – r

Keterangan:
b = jumlah awal (ketika x = 0)
a = faktor penyusutan (0 < a < 1)

r = laju penyusutan per selang waktu T.
y = jumlah setelah selang waktu t
x = fraksi dengan x = tT

• Fungsi Peluruhan Radioaktif

m = m0 × (12)n

Keterangan:
m = massa setelah selang waktu t.
m0 = massa awal
n = tT
t = selang waktu
T = waktu paruh

Mari kita cermati beberapa contoh soal berikut ini.

Contoh 1

Tentukan nilai a jika grafik fungsi f (x) = a x melalui titik:
• P = ( 2, 14)
• Q = (3, 8)

Penyelesaian:

• P = ( 2, 14)

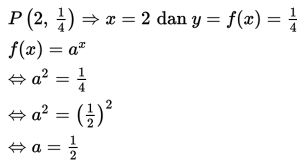
• Q = (3, 8)

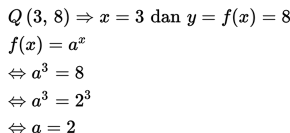
Contoh 2

Diketahui jumlah penduduk Indonesia pada tahun 2010 sekitar 230 juta jiwa dengan laju pertumbuhannya 2% pertahun.
• Tulis persamaan untuk memodelkan jumlah penduduk Indonesia.
• Tentukan jumlah penduduk Indonesia pada tahun 2020.

Penyelesaian:

• Model jumlah penduduk Indonesia.

Oleh karena laju pertumbuhan penduduk = 2% pertahun artinya jumlah penduduk selalu meningkat, maka gunakan fungsi pertumbuhan eksponensial, yaitu:
y = b. a x dengan a = 1 + r

Misal:
b = jumlah penduduk pada tahun 2010 = 230.000.000
r = laju pertumbuhan pertahun = 2% = 0,02
a = faktor pertumbuhan = 1 + r = 1 + 0,02 = 1,02.

Dengan demikian, jumlah penduduk Indonesia bisa dimodelkan sebagai:

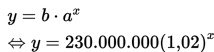
• Pada tahun 2020 berarti:

t = lama waktu pertumbuhan = 2020 – 2010 = 10 tahun
T = selang waktu pertumbuhan = 1 tahun

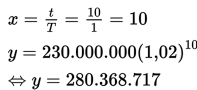
Jadi, jumlah penduduk Indonesia pada tahun 2020 sekitar 280.368.717 jiwa.

Contoh 3

Kolera, penyakit yang menyerang usus, disebabkan oleh bakteri kolera yang berkembang biak secara eksponensial dengan membelah selnya dan dinyatakan dengan N = N0. e 1,386t. N adalah jumlah bakteri yang muncul setelah t jam dan N0 adalah jumlah bakteri pada permulaan (t = 0). Jika di awal terdapat 25 bakteri, tentukan banyak bakteri (dalam satuan terdekat) yang akan muncul dalam waktu:
• 0,6 jam
• 3,5 jam

Penyelesaian:

Substitusikan, N0 = 25 ke persamaan, maka diperoleh
N = 25. e1,386t

• Nilai N ketika t = 0,6

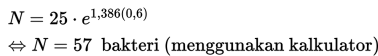
• Nilai N ketika t = 3,5